master
/ 5决策树.ipynb

5决策树.ipynb @96fc089 — view markup · raw · history · blame

Notebook

决策树

1.什么是决策树

决策树是一种通过树形结构进行分类的方法。在决策树中，树形结构中每个节点表示对分类目标在属性上的一个判断，每个分支代表基于该属性做出的一个判断，最后树形结构中每个叶子节点代表一种分类结果。

In [1]:
from IPython.display import IFrame
src = 'http://files.momodel.cn/%E5%86%B3%E7%AD%96%E6%A0%911.pptx'
IFrame('https://view.officeapps.live.com/op/view.aspx?src='+src, width=1200, height=900)
Out[1]:

2.构建决策树

数据: 游乐场经营者提供天气情况（如晴、雨、多云）、温度高低、湿度大小、风力强弱等气象特点以及游客当天是否前往游乐场。

目标: 预测游客是否来游乐场游玩。

序号 天气 温度（℃） 湿度 是否有风 是（1）否（0）前往游乐场
1 晴 29 85 否 0
2 晴 26 88 是 0
3 多云 28 78 否 1
4 雨 21 96 否 1
5 雨 20 80 否 1
6 雨 18 70 是 0
7 多云 18 65 是 1
8 晴 22 90 否 0
9 晴 21 68 否 1
10 雨 24 80 否 1
11 晴 24 63 是 1
12 多云 22 90 是 1
13 多云 27 75 否 1
14 雨 21 80 是 0

下面，我们创建数据并进行一些预处理

In [2]:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import math
from math import log
import warnings
warnings.filterwarnings("ignore")
In [3]:
# 原始数据
datasets = [
    ['晴', 29, 85, '否', '0'],
    ['晴', 26, 88, '是', '0'],
    ['多云', 28, 78, '否', '1'],
    ['雨', 21, 96, '否', '1'],
    ['雨', 20, 80, '否', '1'],
    ['雨', 18, 70, '是', '0'],
    ['多云', 18, 65, '是', '1'],
    ['晴', 22, 90, '否', '0'],
    ['晴', 21, 68, '否', '1'],
    ['雨', 24, 80, '否', '1'],
    ['晴', 24, 63, '是', '1'],
    ['多云', 22, 90, '是', '1'],
    ['多云', 27, 75, '否', '1'],
    ['雨', 21, 80, '是', '0']
]
# 数据的列名
labels = ['天气', '温度', '湿度', '是否有风', '是否前往游乐场']
# 将湿度大小分为大于 75 和小于等于 75 这两个属性值，
# 将温度大小分为大于 26 和小于等于 26 这两个属性值
for i in range(len(datasets)):
    if datasets[i][2] > 75:
        datasets[i][2] = '>75'
    else:
        datasets[i][2] = '<=75'
    if datasets[i][1] > 26:
        datasets[i][1] = '>26'
    else:
        datasets[i][1] = '<=26'
# 构建 dataframe 并查看数据
df = pd.DataFrame(datasets, columns=labels)
df
Out[3]:
天气 温度 湿度 是否有风 是否前往游乐场
0 晴 >26 >75 否 0
1 晴 <=26 >75 是 0
2 多云 >26 >75 否 1
3 雨 <=26 >75 否 1
4 雨 <=26 >75 否 1
5 雨 <=26 <=75 是 0
6 多云 <=26 <=75 是 1
7 晴 <=26 >75 否 0
8 晴 <=26 <=75 否 1
9 雨 <=26 >75 否 1
10 晴 <=26 <=75 是 1
11 多云 <=26 >75 是 1
12 多云 >26 <=75 否 1
13 雨 <=26 >75 是 0
In [4]:
from IPython.display import IFrame
src = 'http://files.momodel.cn/%E5%86%B3%E7%AD%96%E6%A0%9121.pptx'
IFrame('https://view.officeapps.live.com/op/view.aspx?src='+src, width=1200, height=900)
Out[4]:

2.1 信息熵

信息熵用来度量信息量的大小。从信息论的角度来看，对信息的度量等于计算信息不确定性的多少。

In [5]:
from IPython.display import IFrame
src = 'http://files.momodel.cn/%E5%86%B3%E7%AD%96%E6%A0%9123.pptx'
IFrame('https://view.officeapps.live.com/op/view.aspx?src='+src, width=1200, height=900)
Out[5]:

假设有 $K$ 个信息，其组成了集合样本 $D$ ，记第 $k$ 个信息发生的概率为 $p_k(1≤k≤K)$。
这 $K$ 个信息的信息熵：
$$E(D)=-\sum_{k=1}^{K}p_k log_{2} p_k$$

$E(D)$ 的值越小，表示$ D $ 包含的信息越确定，也称$ D $的纯度越高。

需要指出：所有 $p_k$ 累加起来的和为1。

当只有两个信息时，熵随概率变化的曲线如图所示

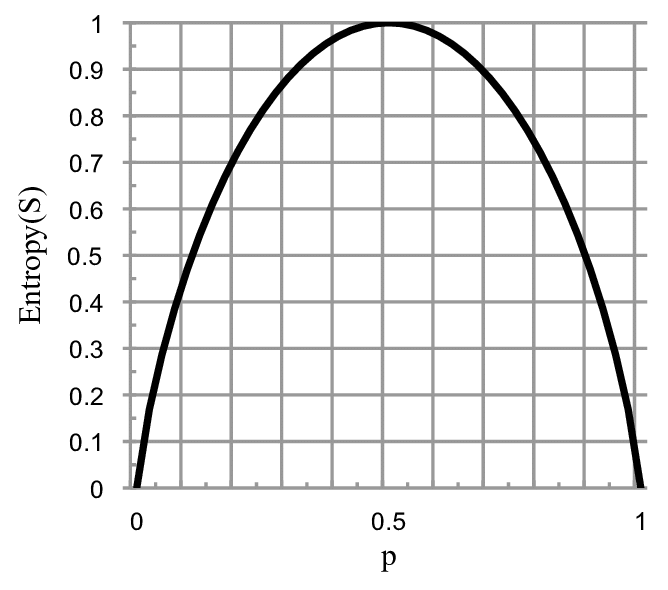
我们来动手实现一下信息熵的计算。 $$E(D)=-\sum_{k=1}^{K}p_k log_{2} p_k$$

In [ ]:
def calc_entropy(total_num, count_dict):
    """
    计算信息熵
    :param total_num: 总样本数, 例如总的样本数是 14
    :param count_dict: 每类样本及其对应数目的字典，例如：{'前往游乐场': 9, '不前往游乐场': 5}
    :return: 信息熵
    """
    
    #初始化 ent 为 0
    
    # 对于每一个类别
    
        # 如果属于该类别的样本数大于 0
        
            # 计算概率
            
            # 计算信息熵
            
    # 返回信息熵，精确到小数点后 3 位
    return round(ent, 3)
In [ ]:
def calc_entropy(total_num, count_dict):
    """
    计算信息熵
    :param total_num: 总样本数, 例如总的样本数是 14
    :param count_dict: 每类样本及其对应数目的字典，例如：{'前往游乐场': 9, '不前往游乐场': 5}
    :return: 信息熵
    """
    
    #初始化 ent 为 0
    ent = 0
    # 对于每一个类别
    for n in count_dict.values():
        # 如果属于该类别的样本数大于 0
        if n > 0:
            # 计算概率
            p = n / total_num
            # 计算信息熵
            ent += - p * log(p, 2)
    # 返回信息熵，精确到小数点后 3 位
    return round(ent, 3)
In [ ]:
df

数据中 14 个样本分为 “游客来游乐场（ 9 个样本）” 和 “游客不来游乐场（ 5 个样本）” 两个类别，即 K = 2。

记 “游客来游乐场” 和 “游客不来游乐场” 的概率分别为 $p_1$ 和 $p_2$ ，显然 $p_1=\frac{9}{14}$，$p_1=\frac{5}{14}$ ，则这 14 个样本所蕴含的信息熵：

$$E(D)=-\sum_{k=1}^{2}p_{k}log_{2}{p_k}=-(\frac{9}{14}×log_{2}{\frac{9}{14}}+\frac{5}{14}×log_{2}{\frac{5}{14}})=0.940$$
In [ ]:
# 样本总数
total_num = 14
# 每类样本的数量
count_dict = {'去游乐场': 9, '不去游乐场': 5}

calc_entropy(total_num, count_dict)

上面我们是一行行数出来的，如何使用代码得到 total_num 和 count_dict ？

In [ ]:
df

我们可以用下面这种方式对 dataframe 的数据按条件进行筛选。

In [ ]:
# 例如：按是否前往游乐场==0 进行筛选
df[df['是否前往游乐场']=='0']

我们可以用下面这种方式对查看数据的行数和列数。

In [ ]:
df.shape

使用上面的方法，可以得到计算信息熵所需的总样本数，以及每类样本及其对应数目的字典，然后计算信息熵。

In [ ]:
# 总样本数
total_num = df.shape[0]

# 前往游乐场的样本数目
num_go_to_play = df[df['是否前往游乐场']=='1'].shape[0]

# 不前往游乐场的样本数目
num_not_go_to_play = df[df['是否前往游乐场']=='0'].shape[0]

# 每类样本及其对应数目的字典
count_dict = {'前往': num_go_to_play,
              '不前往': num_not_go_to_play}

# 计算信息熵
entropy = calc_entropy(total_num, count_dict)
entropy

计算天气状况所对应的信息熵：
天气状况的三个属性记为 $a_0=“晴”$ ，$a_1=“多云”$ ，$a_2=“雨”$ ，
属性取值为 $a_i$ 对应分支节点所包含子样本集记为 $D_i$ ，该子样本集包含样本数量记为 $|D_i|$ 。

天气属性取值$a_i$ “晴” “多云” “雨”
对应样本数$ D_i $ 5 4 5
正负样本数量 （2+，3-） （4+，0-） （3+，2-）

计算天气状况每个属性值的信息熵：

$“晴”：E(D_0)=-(\frac{2}{5}×log_{2}{\frac{2}{5}}+\frac{3}{5}×log_{2}{\frac{3}{5}})=0.971$

$“多云”：E(D_1)=-(\frac{4}{4}×log_{2}{\frac{4}{4}})=0$

$“雨”：E(D_2)=-(\frac{3}{5}×log_{2}{\frac{3}{5}}+\frac{2}{5}×log_{2}{\frac{2}{5}})=0.971$

现在，我们来编写代码进行完成上面的计算。

首先，我们可以使用下面的写法，对 Dataframe 进行多个条件的筛选。

In [ ]:
# 筛选出 天气为晴并且去游乐场的样本数据
df[(df['天气']=='晴') & (df['是否前往游乐场']=='1')]

然后，我们是使用上面的筛选方法，分别计算不同天气下的信息熵。

In [ ]:
# 天气为晴的总天数
total_num_sun = df[df['天气']=='晴'].shape[0]

# 前往游乐场的样本数目
num_go_to_play = df[(df['天气']=='晴') & (df['是否前往游乐场']=='1')].shape[0]

# 不前往游乐场的样本数目
num_not_go_to_play = df[(df['天气']=='晴') & (df['是否前往游乐场']=='0')].shape[0]


# 天气为晴时，去游乐场和不去游乐场的人数
count_dict_sun = {'前往': num_go_to_play ,
                  '不前往': num_not_go_to_play}
print(count_dict_sun)

# 计算天气-晴 的信息熵
ent_sun = calc_entropy(total_num_sun, count_dict_sun)
print('天气-晴 的信息熵为：%s' % ent_sun)
In [ ]:
# 天气为多云的总天数
total_num_cloud = df[df['天气']=='多云'].shape[0]

# 天气为多云时，去游乐场和不去游乐场的人数
count_dict_cloud = {'前往':df[(df['天气']=='多云') & (df['是否前往游乐场']=='1')].shape[0],
                    '不前往':df[(df['天气']=='多云') & (df['是否前往游乐场']=='0')].shape[0]}
print(count_dict_cloud)

# 计算天气-多云 的信息熵
ent_cloud = calc_entropy(total_num_cloud, count_dict_cloud)
print('天气-多云 的信息熵为：%s' % ent_cloud)
In [ ]:
# 天气为雨的总天数
total_num_rain = df[df['天气']=='雨'].shape[0]

# 天气为雨时，去游乐场和不去游乐场的人数
count_dict_rain = {'前往':df[(df['天气']=='雨') & (df['是否前往游乐场']=='1')].shape[0],
              '不前往':df[(df['天气']=='雨') & (df['是否前往游乐场']=='0')].shape[0]}
print(count_dict_rain)

# 计算天气-雨 的信息熵
ent_rain = calc_entropy(total_num_rain, count_dict_rain)
print('天气-雨 的信息熵为：%s' % ent_rain)

2.2 信息增益

信息增益用来衡量样本集合复杂度（不确定性）所减少的程度。

In [ ]:
from IPython.display import IFrame
src = 'http://files.momodel.cn/%E5%86%B3%E7%AD%96%E6%A0%913.pptx'
IFrame('https://view.officeapps.live.com/op/view.aspx?src='+src, width=1200, height=900)

得到不同天气下的信息熵后，我们可以计算天气状况的信息增益:
$$Gain(D,A)=E(D)-\sum_{i}^{n}\frac{|D_i|}{D}E(D)$$

其中，$A=“天气状况”$。于是天气状况这一气象特点的信息增益为： $$Gain(D,天气)=0.940-（\frac{5}{14}×0.971+\frac{4}{14}×0+\frac{5}{14}×0.971）=0.246$$

通常情况下，某个分支的信息增益越大，则该分支对样本集划分所获得的“纯度”越大，信息不确定性减少的程度越大。

我们来编写代码，使用上面的公式计算信息增益。

In [ ]:
# 信息增益
gain = entropy - (total_num_sun / total_num*ent_sun +
                  total_num_cloud / total_num*ent_cloud +
                  total_num_rain / total_num*ent_rain)
round(gain, 3)

同理可以计算温度高低、湿度大小、风力强弱三个气象特点的信息增益。

计算按温度高低进行切分的信息增益。

In [ ]:
# 温度 >26 的信息熵
total_num_temp_high = df[df['温度']=='>26'].shape[0]
count_dict_temp_high = {'前往':df[(df['温度']=='>26') & (df['是否前往游乐场']=='1')].shape[0],
                   '不前往':df[(df['温度']=='>26') & (df['是否前往游乐场']=='0')].shape[0]}
print(count_dict_temp_high)
ent_temp_high = calc_entropy(total_num_temp_high, count_dict_temp_high)
print('温度 >26 的信息熵为：%s' % ent_temp_high)

# 温度 <=26 的信息熵
total_num_temp_low = df[df['温度']=='<=26'].shape[0]
count_dict_temp_low = {'前往':df[(df['温度']=='<=26') & (df['是否前往游乐场']=='1')].shape[0],
                     '不前往':df[(df['温度']=='<=26') & (df['是否前往游乐场']=='0')].shape[0]}
print(count_dict_temp_low)
ent_temp_low = calc_entropy(total_num_temp_low, count_dict_temp_low)
print('温度 <=26 的信息熵为：%s' % ent_temp_low)

# 如果按照温度高低进行划分，则对应的信息增益为
gain = entropy - (total_num_temp_high/total_num*ent_temp_high +
                  total_num_temp_low/total_num*ent_temp_low)
print('按照温度高低进行划分的信息增益为：%s' % gain)

计算按湿度高低进行切分的信息增益。

In [ ]:
# 湿度 >75 的信息熵
total_num_hum_high = df[df['湿度']=='>75'].shape[0]
count_dict_hum_high = {'前往':df[(df['湿度']=='>75') & (df['是否前往游乐场']=='1')].shape[0],
                   '不前往':df[(df['湿度']=='>75') & (df['是否前往游乐场']=='0')].shape[0]}
print(count_dict_hum_high)
ent_hum_high = calc_entropy(total_num_hum_high, count_dict_hum_high)
print('湿度 >75 的信息熵为：%s' % ent_hum_high)

# 湿度 <=75 的信息熵
total_num_hum_low = df[df['湿度']=='<=75'].shape[0]
count_dict_hum_low = {'前往':df[(df['湿度']=='<=75') & (df['是否前往游乐场']=='1')].shape[0],
                     '不前往':df[(df['湿度']=='<=75') & (df['是否前往游乐场']=='0')].shape[0]}
print(count_dict_hum_low)
ent_hum_low = calc_entropy(total_num_hum_low, count_dict_hum_low)
print('湿度 <=75 的信息熵为：%s' % ent_hum_low)

# 如果按照湿度高低进行划分，则对应的信息增益为
gain = entropy - (total_num_hum_high/total_num*ent_hum_high +
                  total_num_hum_low/total_num*ent_hum_low)
print('按照湿度高低进行划分的信息增益为：%s' % gain)

计算按风力强弱进行切分的信息增益。

In [ ]:
# 有风 的信息熵
total_num_wind = df[df['是否有风']=='是'].shape[0]
count_dict_wind = {'前往':df[(df['是否有风']=='是') & (df['是否前往游乐场']=='1')].shape[0],
                   '不前往':df[(df['是否有风']=='是') & (df['是否前往游乐场']=='0')].shape[0]}
print(count_dict_wind)
ent_wind = calc_entropy(total_num_wind, count_dict_wind)
print('有风 的信息熵为：%s' % ent_wind)

# 无风 的信息熵
total_num_nowind = df[df['是否有风']=='否'].shape[0]
count_dict_nowind = {'前往':df[(df['是否有风']=='否') & (df['是否前往游乐场']=='1')].shape[0],
                     '不前往':df[(df['是否有风']=='否') & (df['是否前往游乐场']=='0')].shape[0]}
print(count_dict_nowind)
ent_nowind = calc_entropy(total_num_nowind, count_dict_nowind)
print('无风 的信息熵为：%s' % ent_nowind)

# 如果按照是否有风进行划分，则对应的信息增益为
gain = entropy - (total_num_wind/total_num*ent_wind +
                  total_num_nowind/total_num*ent_nowind)
print('按照是否有风进行划分的信息增益为：%s' % gain)
In [ ]:
from IPython.display import IFrame
src = 'http://files.momodel.cn/%E5%86%B3%E7%AD%96%E6%A0%914.pptx'
IFrame('https://view.officeapps.live.com/op/view.aspx?src='+src, width=1200, height=900)

3. 使用 Sklearn 工具包构建和训练决策树模型

每朵鸢尾花有萼片长度、萼片宽度、花瓣长度、花瓣宽度四个特征。现在需要根据这四个特征将鸢尾花分为杂色鸢尾花（versicolor）、维吉尼亚鸢尾（virginica）和山鸢尾（setosa）三类，试构造决策树进行分类。

序号 萼片长度（sepal length） 萼片宽度（sepal width） 花瓣长度（petal length） 花瓣宽度 （petal width） 种类
1 5.0 2.0 3.5 1.0 杂色鸢尾
2 6.0 2.2 5.0 1.5 维吉尼亚鸢尾
3 6.0 2.2 4.0 1.0 杂色鸢尾
4 6.2 2.2 4.5 1.5 杂色鸢尾
5 4.5 2.3 1.3 0.3 山鸢尾

观察上表中的五笔数据，我们可以看到 杂色鸢尾 和 维吉尼亚鸢尾 的花瓣宽度明显大于 山鸢尾，所以可以通过判断花瓣宽度是否大于 0.7，来将 山鸢尾 从其他两种鸢尾中区分出来。

然后我们观察到 维吉尼亚鸢尾 的花瓣长度明显大于 杂色鸢尾，所以可以通过判断花瓣长度是否大于 4.75，来将 杂色鸢尾 和 维吉尼亚鸢尾区分出来。

上面的表格只是 Iris 数据集的一小部分，完整的数据集包含 150 个数据样本，分为 3 类，每类 50 个数据，每个数据包含 4 个属性。即花萼长度，花萼宽度，花瓣长度，花瓣宽度4个属性。

我们使用 sklearn 工具包来构建决策树模型，先导入数据集。

In [ ]:
from sklearn.datasets import load_iris
# 加载数据集
iris = load_iris()
# 查看 label
print(list(iris.target_names))
# 查看 feature
print(iris.feature_names)

setosa 是山鸢尾，versicolor是杂色鸢尾，virginica是维吉尼亚鸢尾。

sepal length， sepal width，petal length，petal width 分别是萼片长度，萼片宽度，花瓣长度，花瓣宽度。

然后进行训练集和测试集的切分。

In [ ]:
from sklearn.model_selection import train_test_split
# 按属性和标签载入数据
X, y = load_iris(return_X_y=True)
# 切分训练集合测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)

接下来，我们在训练集数据上训练决策树模型。

In [ ]:
from sklearn import tree
from sklearn.tree import DecisionTreeClassifier
# 初始化模型，可以调整 max_depth 来观察模型的表现， 
# 也可以调整 criterion  为 gini 来使用 gini 指数构建决策树
clf = tree.DecisionTreeClassifier()
# 训练模型
clf = clf.fit(X_train, y_train)

我们可以使用 graphviz 包来展示构建好的决策树。

In [ ]:
import graphviz
feature_names = ['萼片长度','萼片宽度','花瓣长度','花瓣宽度']
target_names = ['山鸢尾', '杂色鸢尾', '维吉尼亚鸢尾']
# 可视化生成的决策树
dot_data = tree.export_graphviz(clf, out_file=None,
                     feature_names=feature_names,
                     class_names=target_names,
                     filled=True, rounded=True,
                     special_characters=True)
graph = graphviz.Source(dot_data)
graph

我们看模型在测试集上的表现

In [ ]:
from sklearn.metrics import accuracy_score
y_test_predict = clf.predict(X_test)
accuracy_score(y_test,y_test_predict)

4. 扩展内容

4.1 基尼指数

除了使用信息增益以外，我们也可以使用基尼指数来构建决策树。

分类问题中，假设有 $K$ 个类，样本点属于第 $k$ 类的概率为 $p_{k}$，则概率分布的基尼指数定义为：

$$\operatorname{Gini}(p)=\sum_{k=1}^{K} p_{k}\left(1-p_{k}\right)=1-\sum_{k=1}^{K} p_{k}^{2}$$

对于给定的样本集合 $D$，其基尼指数为

$$\operatorname{Gini}(D)=1-\sum_{k=1}^{K}\left(\frac{\left|C_{k}\right|}{|D|}\right)^{2}$$

这里，$C_{k}$ 是 $D$ 中属于第 $k$ 类的样本子集，$K$ 是类的个数。

如果样本集合 $D$ 根据特征 $A$ 是否取某一可能值 $a$ 被分割为 $D_{1}$ 和 $D_{2}$ 两部分，即

$$D_{1}=\{(x, y) \in D | A(x)=a\}, \quad D_{2}=D-D_{1}$$

则在特征 $A$ 的条件下，集合 $D$ 的基尼指数定义为

$$\operatorname{Gini}(D, A)=\frac{\left|D_{1}\right|}{|D|} \operatorname{Gini}\left(D_{1}\right)+\frac{\left|D_{2}\right|}{|D|} \operatorname{Gini}\left(D_{2}\right)$$

基尼指数 $Gini(D)$ 表示集合 $D$ 的不确定性，基尼指数 $Gini(D, A)$ 表示经过分割后集合 $D$ 的不确定性。基尼指数值越大，样本集合的不确定性也就越大，这一点与信息熵相似。

想一想：

对于二分类问题，若样本点属于第 1 个类的概率是 $p$，则概率分布的基尼指数是多少？

$$\text { Gini }(p)=2 p(1-p)$$

4.2 计算文章的信息熵

收集中英文对照的短文，在计算短文内中文单词和英文单词出现概率基础上，计算该两篇短文的信息熵，比较中文短文信息熵和英文短文信息熵的大小。

首先定义一个方法来辅助读取文件的内容。

In [ ]:
def read_file(path):
    """
    读取某文件的内容
    :param path: 文件的路径
    :return: 文件的内容
    """
    contents = ""
    with open(path) as f:
        # 读取每一行的内容
        for line in f.readlines():
            contents += line
    return contents

使用上面定义的方法读取英文短文及其对应的中文短文。

In [ ]:
# 读取英文短文
en_essay = read_file('essay1_en.txt')
# 读取中文短文
ch_essay = read_file('essay1_ch.txt')
In [ ]:
en_essay
In [ ]:
ch_essay

处理文本，统计单词出现的概率，并计算信息熵。

In [ ]:
from collections import Counter
import re


def cal_essay_entropy(essay, split_by=None):
    """
    计算文章的信息熵
    :param essay: 文章内容
    :param split_by: 切分方式，对于中文文章，不需传入，按字符切分，
                     对于英文文章，需传入空格字符来进行切分
    :return: 文章的信息熵
    """
    # 把英文全部转为小写
    essay = essay.lower()
    # 去除标点符号
    essay = re.sub(
        "[\f+\n+\r+\t+\v+\?\.\!\/_,$%^*(+\"\']+|[+——！，。？、~@#《》￥%……&*（）]", "",
        essay)
    # print(essay)
    # 把文本分割为词
    if split_by:
        word_list = essay.split(split_by)
    else:
        word_list = list(essay)
    # 统计总的单词数
    word_number = len(word_list)
    print('此文章共有 %s 个单词' % word_number)
    # 得到每个单词出现的次数
    word_counter = Counter(word_list)
    # print('每个单词出现的次数为：%s' % word_counter)
    # 使用信息熵公式计算信息熵
    ent = -sum([(p / word_number) * log(p / word_number, 2) for p in
                word_counter.values()])
    print('信息熵为：%.2f' % ent)
    return ent
In [ ]:
ent = cal_essay_entropy(ch_essay)
In [ ]:
ent = cal_essay_entropy(en_essay, split_by = ' ')

5.扩展阅读

  1. 决策树与随机森林
  2. 从决策树到随机森林：树型算法的原理与实现
  3. sklearn 决策树