2.5 神经网络学习

神经网络模拟人脑神经元的连接来达到学习功能，通过逐层抽象将输入数据逐层映射为概念等高等语义。

2.5.1 人脑神经机制

人眼在辨识图片时，会先提取边缘特征，再识别部件，最后再得到最高层的模式。也就是说，高层的特征是低层特征的组合，从低层到高层的特征表示越来越抽象，越来越能表现语义。

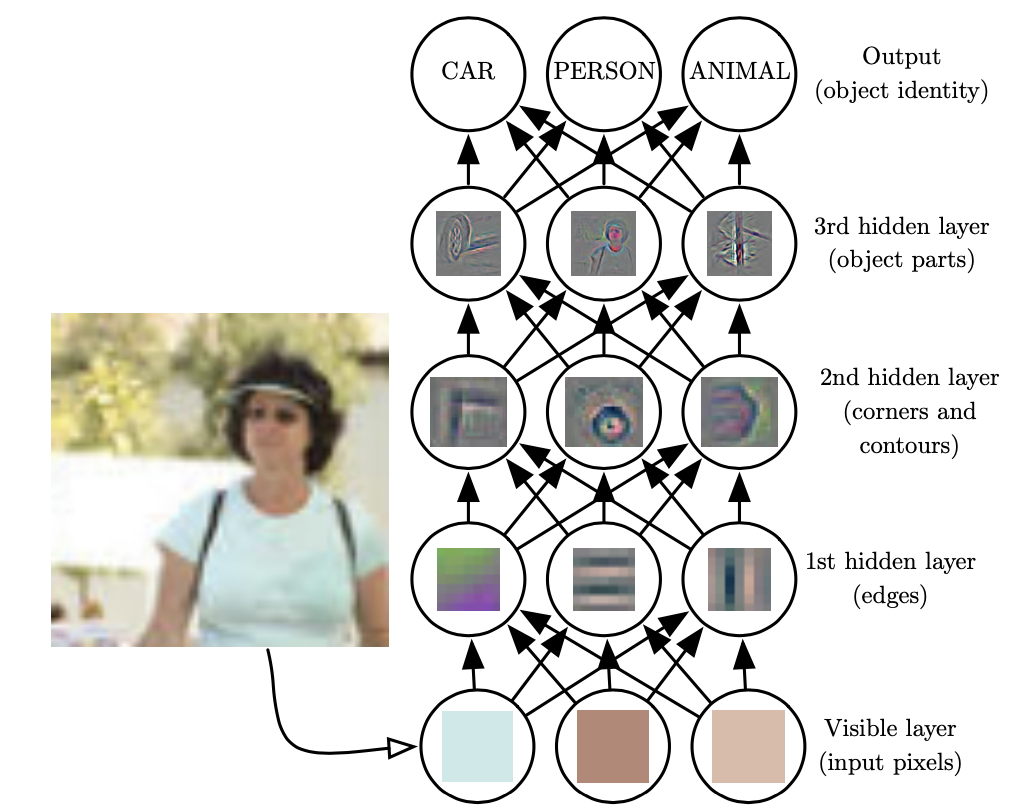
2.5.2 感知机模型

感知机模型：

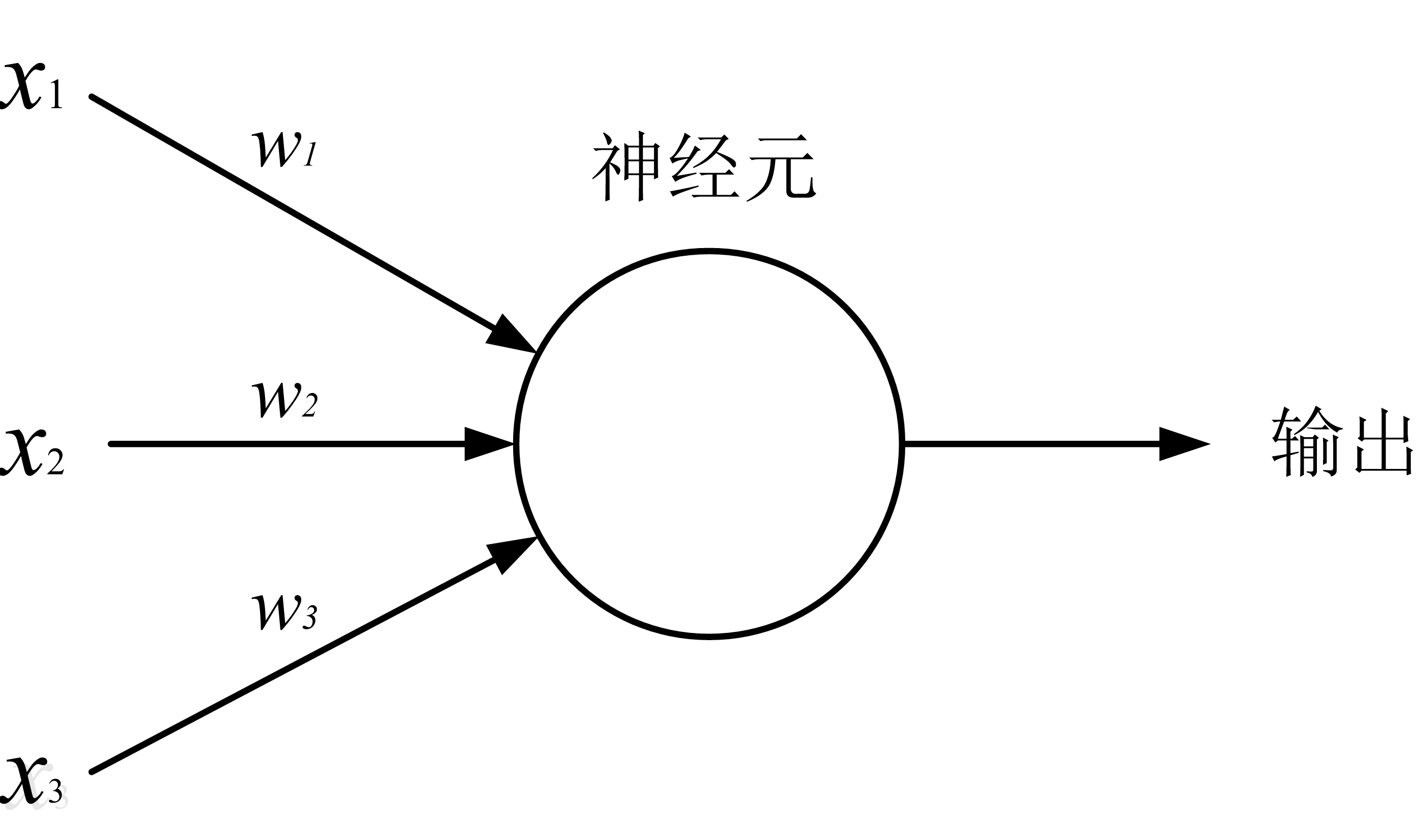
输入项：3个，$x_1,x_2,x_3$
神经元：1个，用圆圈表示
权重：每个输入项均通过权重与神经元相连（比如 $w_i$ 是 $x_i$ 与神经元相连的权重）
输出：1个

工作方法：

• 计算输入项传递给神经元的信息加权总和，即：$y_{sum} = w_1x_1+w_2x_2+w_3x_3$
• 如果 $y_{sum}$ 大于某个预定阀值（比如 0.5），则输出为 1，否则为 0 。

在输出的判断上，其实不仅可以简单的按照阈值来判断，可以通过一个函数来进行计算，这个函数称为激活函数。常见的激活函数有： sigmoid，tanh，relu 等。下面我们看看这些激活函数的曲线图。

import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")


def plot_activation_function(activation_function):
    """
    绘制激活函数
    :param activation_function: 激活函数名
    :return:
    """
    x = np.arange(-10, 10, 0.1)
    y_activation_function = activation_function(x)

    # 绘制坐标轴
    ax = plt.gca()
    ax.spines['right'].set_color('none')
    ax.spines['top'].set_color('none')
    ax.xaxis.set_ticks_position('bottom')
    ax.yaxis.set_ticks_position('left')
    ax.spines['bottom'].set_position(('data', 0))
    ax.spines['left'].set_position(('data', 0))

    # 绘制曲线图
    plt.plot(x, y_activation_function)
    
    # 展示函数图像
    plt.show()

def sigmoid(x):
    """
    sigmoid函数
    :param x: np.array 格式数据
    :return: sigmoid 函数
    """
    return 1 / (1 + np.exp(-x))

# 绘制 sigmoid 函数图像
plot_activation_function(sigmoid)

def tanh(x):
    """
    tanh函数
    :param x: np.array 格式数据
    :return: tanh 函数
    """
    return ((np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x)))

# 绘制 tanh 函数图像
plot_activation_function(tanh)

def relu(x):
    """
    relu 函数
    :param x: np.array 格式数据
    :return: relu 函数
    """
    temp = np.zeros_like(x)
    if_bigger_zero = (x > temp)
    return x * if_bigger_zero

# 绘制 relu 函数
plot_activation_function(relu)

我们根据上面的定义可以编写一个简单的感知机模型。

def perceptron(x, w, threshold):
    """
    感知机模型
    :param x: 输入数据 np.array 格式
    :param w: 权重 np.array 格式，需要与 x 一一对应
    :param threshold: 阀值
    :return: 0或者1
    """
    x = np.array(x)
    w = np.array(w)
    y_sum = np.sum(w * x)
    # 大于阀值返回 1，否则返回 0
    return 1 if y_sum > threshold else 0


# 输入数据
x = np.array([1, 1, 4])
# 输入权重
w = np.array([0.5, 0.2, 0.3])
# 返回结果
perceptron(x, w, 0.8)

2.5.3 神经网络

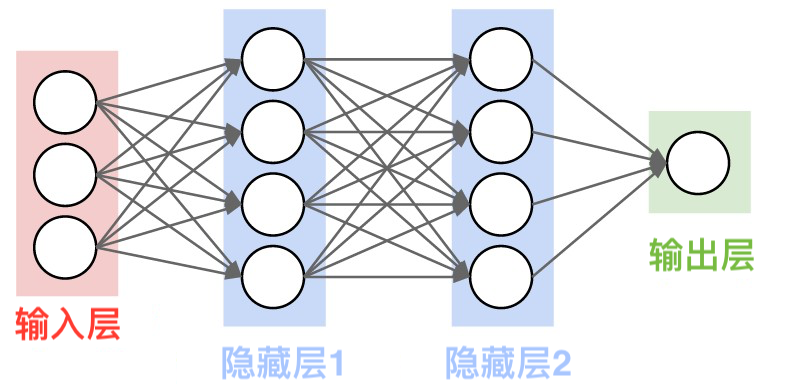
与感知机的不同，神经网络：

• 输入层和输出层之间存在若干隐藏层。
• 每个隐藏层中包含若干神经元。

2.5.4 搭建神经网络

采用 keras 框架搭建一个神经网络解决手写体数字识别问题。

1. 导入相关包

import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers.core import Dense,Activation,Dropout
from keras.utils import np_utils
import warnings
warnings.filterwarnings("ignore")
!mkdir -p ~/.keras/datasets
!cp ./mnist.npz ~/.keras/datasets/mnist.npz

1. 下载 MNIST 数据集并将它们转换为模型所能使用的格式。

# 获取数据
(X_train, y_train),(X_test,y_test) = mnist.load_data()

# 将训练集数据形状从（60000,28,28）修改为（60000,784）
X_train = X_train.reshape(len(X_train),-1)
X_test = X_test.reshape(len(X_test),-1)

# 将数据集图像像素点的数据类型从 uint8 修改为 float32
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')

# 把数据集图像的像素值从 0-255 放缩到[-1,1]之间
X_train = (X_train - 127)/127
X_test = (X_test - 127)/127

# 数据集类别个数
nb_classes = 10

# 把 y_train 和 y_test 变成了 one-hot 的形式，即之前是 0-9 的一个数值， 
# 现在是一个大小为 10 的向量，它属于哪个数字，就在哪个位置为 1，其他位置都是 0。
y_train = np_utils.to_categorical(y_train,nb_classes)
y_test = np_utils.to_categorical(y_test,nb_classes)

1. 搭建神经网络模型

def create_model():
    """
    采用 keras 搭建神经网络模型
    :return: 神经网络模型
    """
    # 选择模型，选择序贯模型（Sequential())
    model = Sequential()
    
    # 添加全连接层，共 512 个神经元
    model.add(Dense(512,input_shape=(784,),kernel_initializer='he_normal'))
    
    # 添加激活层，激活函数选择 relu 
    model.add(Activation('relu'))
    
    # 添加全连接层，共 512 个神经元
    model.add(Dense(512,kernel_initializer='he_normal'))
    
    # 添加激活层，激活函数选择 relu 
    model.add(Activation('relu'))
    
    # 添加全连接层，共 10 个神经元
    model.add(Dense(nb_classes))
    
    # 添加激活层，激活函数选择 softmax
    model.add(Activation('softmax'))
    
    return model

model = create_model()

1. 训练和测试神经网络模型

def fit_and_predict(model, model_path):
    """
    训练模型、模型评估、保存模型
    :param model: 搭建好的模型
    :param model_path:保存模型路径
    :return:
    """
    # 编译模型
    model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
    
    # 模型训练
    model.fit(X_train, y_train, epochs=5, batch_size=64, verbose=1, validation_split=0.05)
    
    # 保存模型
    model.save(model_path)
    
    # 模型评估，获取测试集的损失值和准确率
    loss, accuracy = model.evaluate(X_test, y_test)

    # 打印结果
    print('Test loss:', loss)
    print("Accuracy:", accuracy)

# 训练模型和评估模型
fit_and_predict(model, model_path='./model.h5')

实践与体验

调节神经网络结构和参数

1. 将两层隐藏层改为一层，训练模型并在测试集上测试，得出准确率。

def create_model1():
    """
    搭建神经网络模型 model1，比 model 少一层隐藏层
    :return: 模型 model1
    """
    # 选择模型，选择序贯模型（Sequential())
    model = Sequential()

    # 添加全连接层，共 512 个神经元
    model.add(Dense(512, input_shape=(784,), kernel_initializer='he_normal'))

    # 添加激活层，激活函数选择 relu
    model.add(Activation('relu'))

    # 添加全连接层，共 10 个神经元
    model.add(Dense(nb_classes))

    # 添加激活层，激活函数选择 softmax
    model.add(Activation('softmax'))

    return model

# 搭建神经网络
model1 = create_model1()

# 训练神经网络模型，保存模型和评估模型
fit_and_predict(model1, model_path='./model1.h5')

1. 修改两层隐藏层神经元的数量，然后训练模型得出准确率。

def create_model2():
    """
    搭建神经网络模型 model2，隐藏层的神经元数目比 model 少一半
    :return: 神经网络模型 model2
    """
    # 选择模型，选择序贯模型（Sequential())
    model = Sequential()

    # 添加全连接层，共 256 个神经元
    model.add(Dense(256, input_shape=(784,), kernel_initializer='he_normal'))

    # 添加激活层，激活函数选择 relu
    model.add(Activation('relu'))

    # 添加全连接层，共 256 个神经元
    model.add(Dense(256, kernel_initializer='he_normal'))

    # 添加激活层，激活函数选择 relu
    model.add(Activation('relu'))

    # 添加全连接层，共 10 个神经元
    model.add(Dense(nb_classes))

    # 添加激活层，激活函数选择 softmax
    model.add(Activation('softmax'))

    return model

# 搭建神经网络模型
model2 = create_model2()

# 训练神经网络模型，保存模型并评估模型
fit_and_predict(model2,model_path='./model2.h5')

1. 输入一个手写数字，比较三种模型输出结果的差异，对其差异进行分析解释。

import numpy as np
np.set_printoptions(suppress=True)
from keras.models import load_model

# 加载模型
model = load_model('./model.h5')
model1 = load_model('./model1.h5')
model2 = load_model('./model2.h5')  

# 预测结果
predict_results = np.round(model.predict(X_test)[0],3)
predict_results1 = np.round(model1.predict(X_test)[0],3)
predict_results2 = np.round(model2.predict(X_test)[0],3)

# 打印预测结果
print('原始模型\n其各类别预测概率:%s，预测值: %s，真实值:%s\n'  % (predict_results,np.argmax(predict_results),np.argmax(y_test[0])))
print('只有一个隐藏层的模型\n其各类别各类别预测概率:%s，预测值: %s，真实值:%s\n'  % (predict_results1,np.argmax(predict_results1),np.argmax(y_test[0])))
print('隐藏神经元数量更改后的模型\n其各类别预测概率:%s，预测值: %s，真实值:%s'  % (predict_results2,np.argmax(predict_results2),np.argmax(y_test[0])))