线性回归¶

1.线性回归介绍¶

我们先来看一段视频，了解什么是线性回归，并了解一些监督学习相关的概念。

我们刚才以房价预测例子，介绍了线性回归、监督学习、训练集等相关的概念。
看看下面这张图，回忆一下刚才讲的内容，数据集中的输入输出分别是什么？

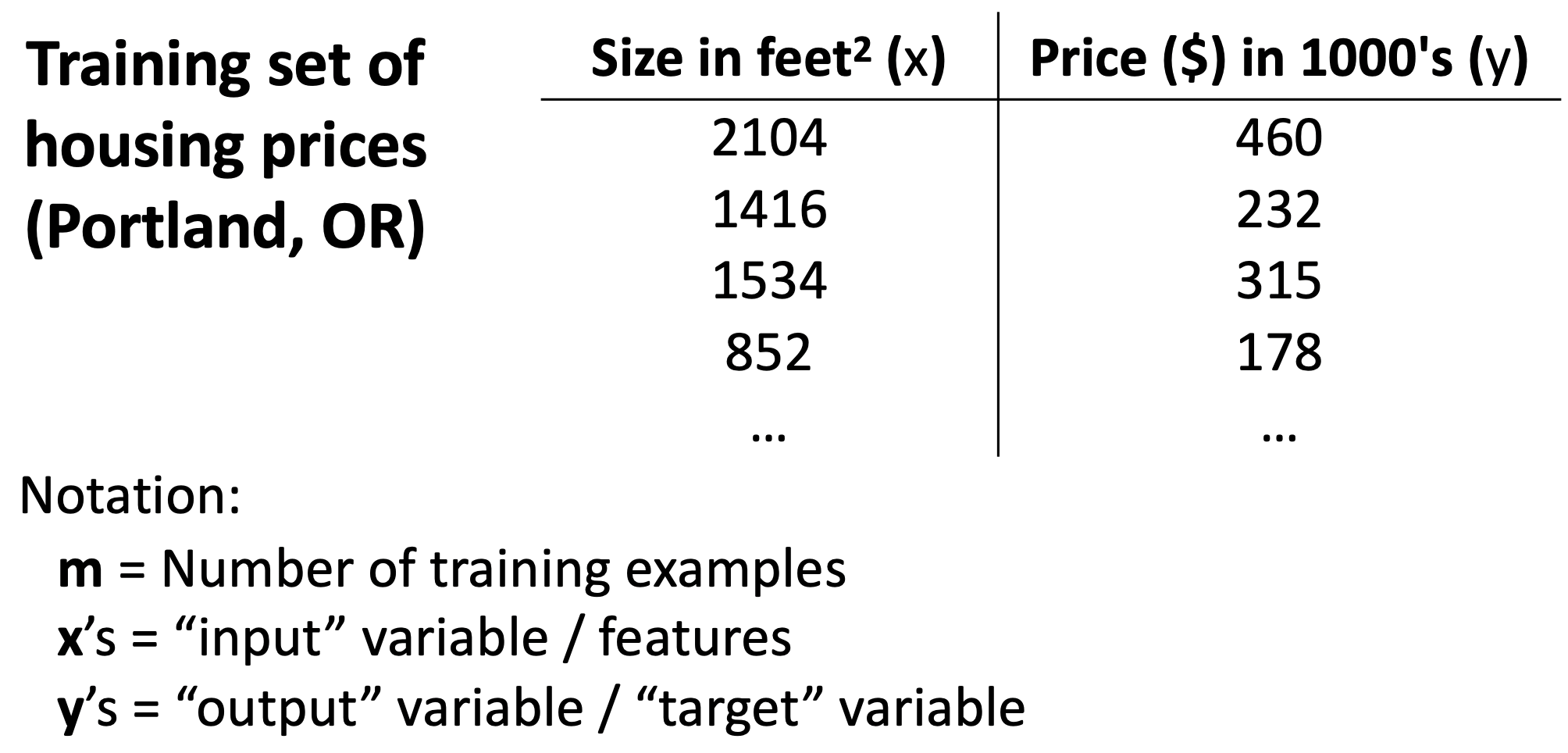
如果现在有一个房子 H1，面积是 S，监督学习如何估算它的价格？

监督学习从训练集中找到面积最接近 S 的房子 H2，预测 H1 的价格等于 H2 的价格
监督学习根据训练集，找到一个数学表达式，对任意的面积的房子都可以估算出其价格

监督学习会采用上面的哪一种方案呢？

2.监督学习的一般流程¶

我们刚才了解了监督学习算法是怎么工作的，并且理解了代价函数的含义。

3.模型假设¶

看看下面这张图，回忆一下刚才讲的内容，图中的 h 代表假设函数，我们怎么构建一个合理的假设函数?

在设计假设函数的时候需要考虑那些因素，本章节将带领大家解决这些问题。

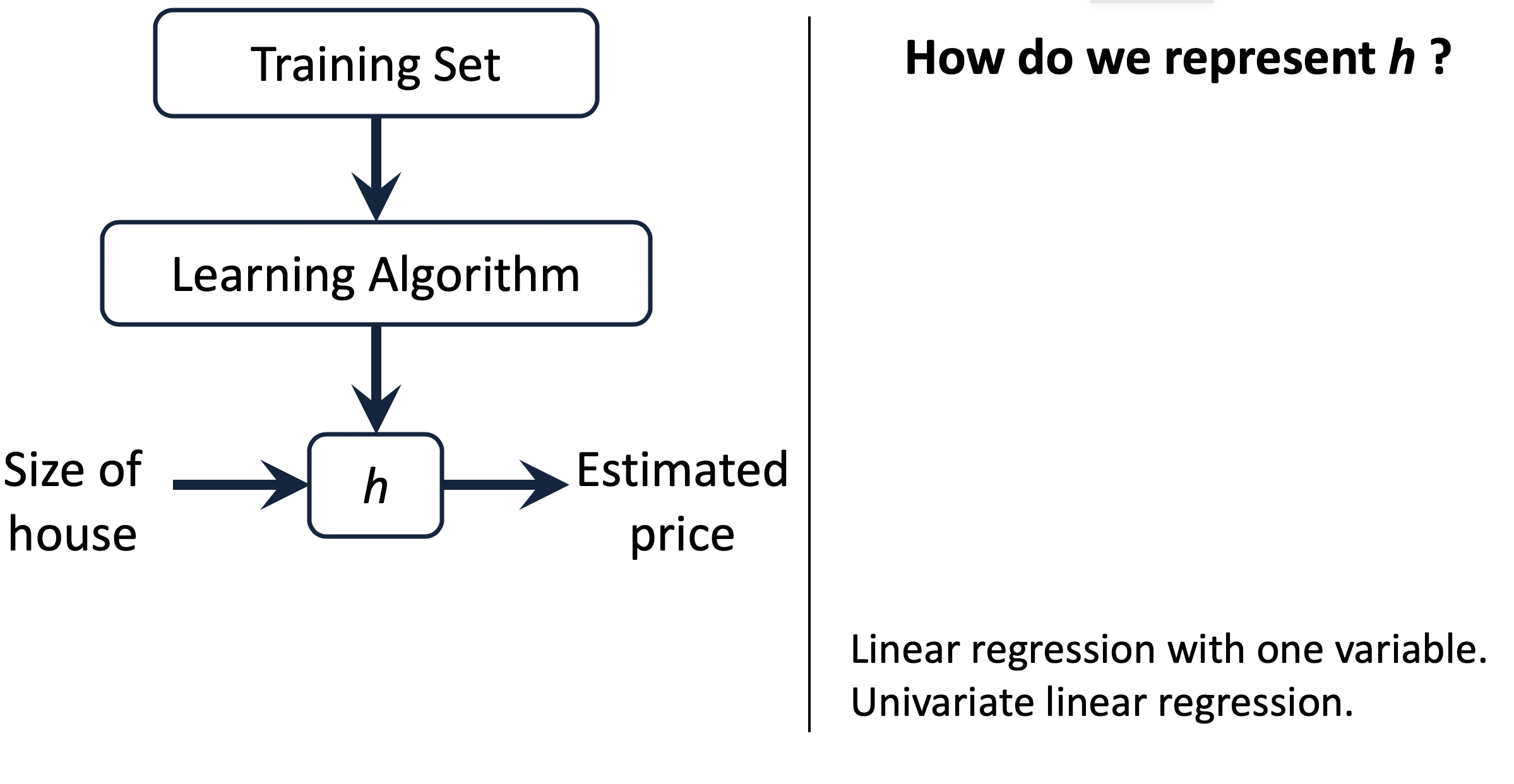
下面，我们对这三个表达式进行绘图，你可以尝试修改 a，b，c 的值来观察绘图的变化情况。

# 导入绘图需要的包
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

def plot_lines(a, b, c):
    x = np.linspace(0, 5, 50)
    # 进行绘图
    plt.figure(dpi=100)
    plt.plot(x, b*x+c, label='bx + c')
    plt.plot(x, b*x, label='bx')
    plt.plot(x, a*x*x+b*x+c, label='ax^2 + bx + c')
    plt.legend()
    plt.show()

from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets

# 拖拽修改参数 a, b, c 的值来观察绘图的变化情况
interact(plot_lines,
         a=widgets.FloatSlider(min=-10, max=10, step=0.5, value=1),
         b=widgets.FloatSlider(min=-10, max=10, step=0.5, value=1),
         c=widgets.FloatSlider(min=-10, max=10, step=0.5, value=1),
        );

# 运行下面的代码，查看问题并回答
from widget_help import question1
question1()

我们刚才了解了线性回归模型中的模型假设，所以得到的线性回归的假设函数是：

$h_{\theta}(x)=\theta_{0}+\theta_{1} x$

模型求解¶

那么我们如何得到合适的 $\theta_{0}$ 和 $\theta_{1}$ 呢？

我们有两种解决思路：

尝试一些 $\theta_{0}$ 和 $\theta_{1}$ 的组合，选择能使得画出的直线正好穿过训练集的 $\theta_{0}$ 和 $\theta_{1}$。
尝试一些 $\theta_{0}$ 和 $\theta_{1}$ 的组合，然后在训练集上进行预测，选能使得预测值与真实的房子价格最接近的 $\theta_{0}$ 和 $\theta_{1}$。

刚才我们看到了根据不同的 $\theta_{0}$ 和 $\theta_{1}$ 绘制出的直线是不同的。

我们现在希望能选择最佳的 $\theta_{0}$ 和 $\theta_{1}$，使得 $h_{\theta}(x)$ 对所有的训练样本 $(x, y)$ 来说，尽可能的接近 $y$。

我们该如何将其转化为数学表达呢？你认为它是下面三种表达式中的哪一种呢？

$minimize \frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}$
$minimize \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)$
$minimize \frac{1}{m} \sum_{i=1}^{m}\left|h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right|$

刚才我们了解选择最小化 $ \frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}$ 得到的 $\theta_{0}$ 和 $\theta_{1}$ 是最佳的。

现有 4 个房屋的面积和价格数据，和一个线性回归模型 $h_{\theta}(x)=\theta_{0}+\theta_{1} x$。

现在让我们调整参数 $\theta_{0}$，$\theta_{1}$ ，观察线性回归模型的绘图情况，及对应的“损失”是多少。

# 房屋的价格和面积数据
import numpy as np
data = np.array([[2104, 460], [1416, 232], [1534, 315], [852,178]])

我们现在知道了线性回归的模型就是

$h_{\theta}(x)=\theta_{0}+\theta_{1} x$

试试看按照公式补全下方代码

# 使用线性回归模型计算预测值
def get_predict(x, theta0, theta1):
    #todo 
    return

问题提示插入答案

编程实现计算损失函数值

# 计算损失值
def cal_cost(theta0, theta1):
    cost = 0
    for x, y in data:
        y_pred = get_predict(x, theta0, theta1)
        cost += (y_pred - y)**2
    return round(cost/len(data)/2, 2)

利用 matplotlib 绘图工具包，绘制不同参数值下，房屋面积和房屋价格的关系图。

# 导入绘图需要的包
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

def plot_cost(theta0, theta1):
    x = np.linspace(0, 2500, 50)
    # 进行绘图
    plt.figure(dpi=100)
    plt.plot(x, get_predict(x, theta0, theta1),
             label='theta0=' + str(theta0) + ',theta1='+ str(theta1)
             + ',cost='+ str(cal_cost(theta0=theta0, theta1=theta1)))
    plt.plot(data[:,0],data[:,1], 'bo')
    plt.legend()
    plt.xlabel("面积")
    plt.ylabel("价格")
    plt.show()

from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets

# 拖拽修改参数 theta0，theta1 的值来观察绘图的变化情况
interact(plot_cost,
         theta0=widgets.IntSlider(min=-200, max=200, step=10, value=10),
        theta1=widgets.FloatSlider(min=-1.0, max=1.0, step=0.05, value=0.3));

代价函数与梯度下降算法¶

根据房价预测例子，我们抽象出假设函数（Hypothesis），模型参数（Parameters），代价函数（Cost Function），优化目标（Goal）。

为理解方便，下面讲解中将 h 函数简化为 $h_{0}(x) =\theta_{1}x$，即设 $\theta_{0}=0$ 。由此我们可以画出假设 h 和优化函数 $J(\theta)$ 对应的函数图像。

通过图像，我们可以很清楚的理解假设函数和代价函数之间的对应关系

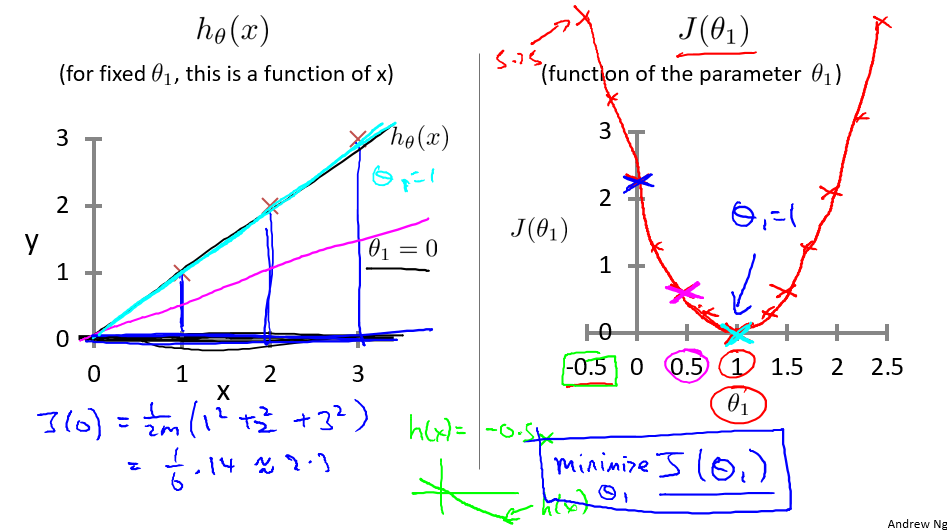
我们假设 $\theta_0=0$，仅考虑了 $\theta_1$, 得到的图像是一个弓形曲线。如果我们考虑 $[\theta_0, \theta_1]$ 两个参数，得到的图像是什么样子呢？

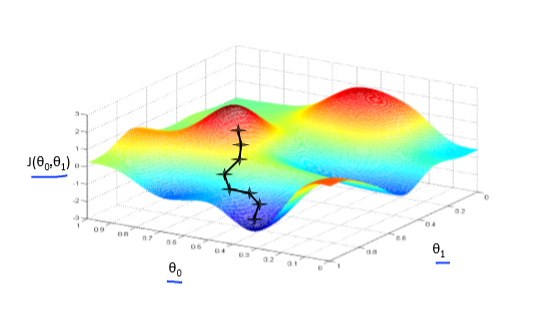
我们刚才通过三维可视化来理解有两个参数情况下，假设函数和代价函数的关系。

从代价函数的可视化图像（下图所示）中可以看出在三维空间中存在一个使得 $J(\theta_{0}, \theta_{1})$最小的点。

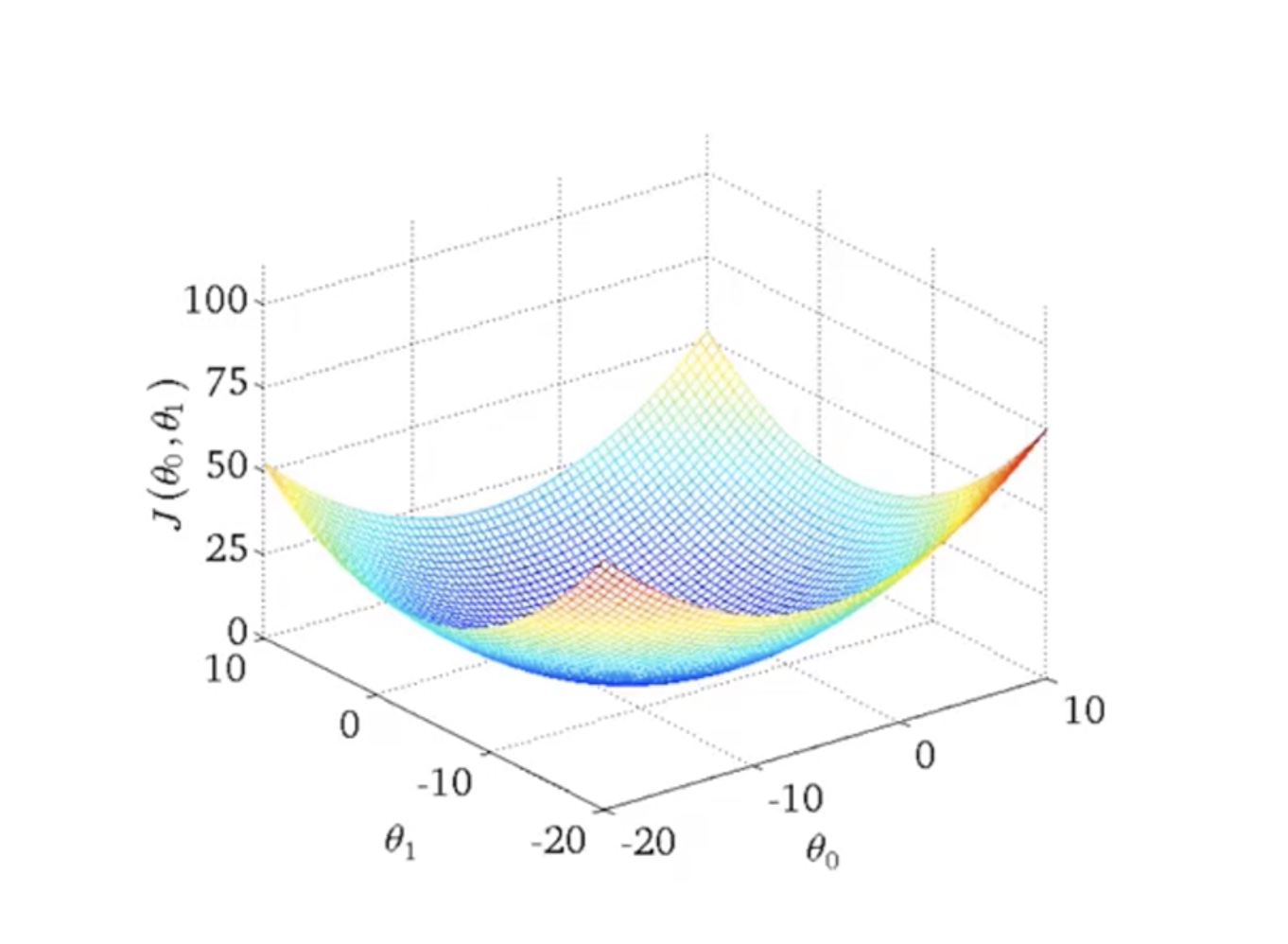
通过可视化方法，希望你能更好地理解这些代价函数 $J$ 所表达的值是什么样的，它们对应的假设是什么样的，以及什么样的假设对应的点，更接近于代价函数 $J$ 的最小值。

当然，我们真正需要的是一种有效的算法，能够自动地找出这些使代价函数 $J$ 取最小值的参数 $\theta_{0}$ 和 $\theta_{1}$。

我们也不希望编程序把这些点画出来，然后人工的方法来读出这些点的数值，这很明显不是一个好办法。
我们会遇到更复杂、更高维度、更多参数的情况，而这些情况是很难画出图的，也就是很难将其可视化。
因此我们真正需要的是编写程序来找出这些最小化代价函数的 $\theta_{0}$ 和 $\theta_{1}$ 的值。

梯度下降是一个用来求函数最小值的算法，我们将使用梯度下降算法来求出代价函数$J(\theta_{0}, \theta_{1})$的最小值。

通过前面的视频，我们先来理解一下使用梯度下降算法求解代价函数最小值的问题概述和具体过程。

我们先来通过视频直观的理解梯度下降求解最小值的思想。

梯度下降背后的思想是：开始时我们随机选择一个参数的组合 $(\theta_{0},\theta_{1},......,\theta_{n})$ ，
计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。

我们持续这么做直到抵达一个局部最小值（local minimum），因为我们并没有尝试完所有的参数组合，
所以不能确定我们得到的局部最小值是否便是全局最小值（global minimum），选择不同的初始参数组合，
可能会找到不同的局部最小值。

现在我们来看一下梯度下降算法背后的数学原理，这部分的理解需要一些简单微积分知识，
如果对微积分的知识不了解也不用担心，跟着视频的思路也能很好的理解梯度下降算法。

细节注意：更新$\theta_{0}$和 $\theta_{1}$。

实现梯度下降算法的微妙之处是，在这个表达式中，如果你要更新这个等式，需要同时更新 $\theta_{0}$和 $\theta_{1}$，
实现方法是：你应该计算公式右边的部分，通过那一部分计算出$\theta_{0}$和 $\theta_{1}$的值，然后同时更新$\theta_{0}$和$\theta_{1}$。

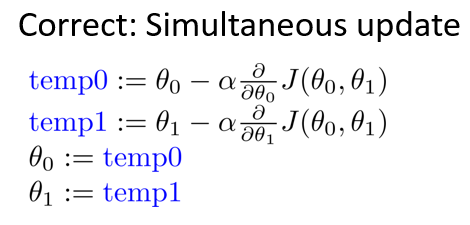
在梯度下降算法中，这是正确实现同时更新的方法。注意区别不正确的写法：

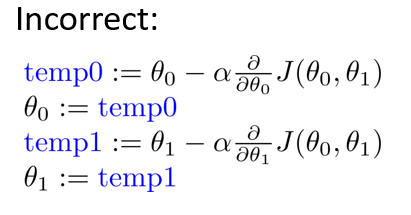
接下来我们来更深入的理解梯度下降算法是干什么的以及梯度下降算法更新过程有什么意义。

高能预警！开启烧脑模式！

这里面需要注意的是，学习率 $\alpha$ 如何选择。

让我们来看看如果 $\alpha$ 太小或 $\alpha$ 太大会出现什么情况：

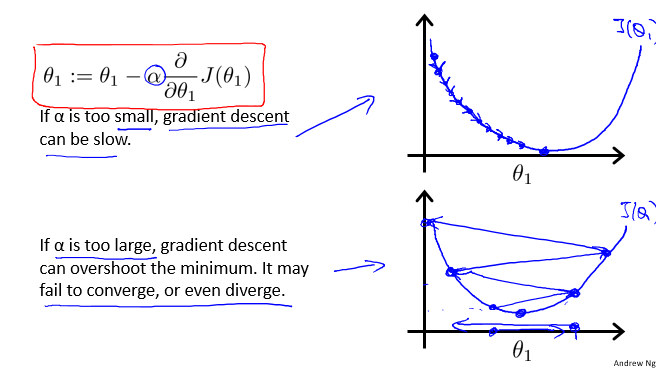
如果 $\alpha$ 太小或 $\alpha$ 太大会出现什么情况

如果 $\alpha$ 太小了，即我的学习速率太小，可能会很慢，因为它会一点点挪动，它会需要很多步才能到达全局最低点。
如果 $\alpha$ 太大，那么梯度下降法可能会越过最低点，下一次迭代又移动了一大步，越过一次，又越过一次，一次次越过最低点，直到你发现实际上离最低点越来越远，最终会导致无法收敛，甚至发散。

前面我们讲解了代价函数的含义，线性回归模型和梯度下降算法。

接下来我们要结合梯度下降和代价函数，完成线性回归算法建模，得到预测房屋价格的模型。

在上面这段视频中，我们要将梯度下降应用于具体的拟合直线的线性回归算法里。

梯度下降算法和线性回归算法，如图：

对我们之前的线性回归问题运用梯度下降法，关键在于求出代价函数的导数，即： $$\frac{\partial}{\partial{\theta_{j}}}J(\theta_{0}, \theta_{1}) = \frac{\partial}{\partial{\theta_{j}}}\frac{1}{2m}\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})^{2}$$

$$j=0 时： \frac{\partial}{\partial{\theta_{0}}}J(\theta_{0}, \theta_{1}) = \frac{1}{m}\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})$$

$$j=1 时：\frac{\partial}{\partial{\theta_{1}}}J(\theta_{0}, \theta_{1}) = \frac{1}{m}\sum_{i=1}^m((h_{\theta}(x^{(i)})-y^{(i)})*x^{(i)})$$

则算法改写成：

以上视频讲解了梯度下降算法在线性回归中的应用及假设函数的拟合效果和代价函数的对应关系。

我们刚刚使用的算法，被称为批量梯度下降。它指的是在梯度下降的每一步中，都用到了所有的训练样本，
在计算微分求导项时，需要进行求和运算。
所以，在每一个单独的梯度下降中，都需要对所有m个训练样本求和。
而事实上，也有其他类型的梯度下降法每次只关注训练集中的一些小的子集，后面的课程中会详细介绍。